|
|||||
REVISTA TRIPLOV
|
|||||
|
Um código é um sistema de probabilidade que reduz a equiprobabilidade original. Umberto Eco [*] En général l’espace de genre G est en plus catégorisé en espèces (…) par un potentiel V : G→R3. Les bassins d’attraction des minima définissent alors les catégories (les espèces) de G et les minima fonctionnent comme des prototypes. Jean Petitot [&] É finalmente a satisfação intelectual à vista do modelo que é o critério último da sua validade. René Thom transcrito em Rosa Branco [§] |
|||||
EDITOR | TRIPLOV |
|||||
| ISSN 2182-147X | |||||
| Dir. Maria Estela Guedes | |||||
| Página Principal | |||||
| Índice de Autores | |||||
| Série Anterior | |||||
| SÍTIOS ALIADOS | |||||
| TriploII - Blog do TriploV | |||||
| Agulha Hispânica | |||||
| Filo-cafés | |||||
| O Bule | |||||
| Jornal de Poesia | |||||
| Agulha Hispânica | |||||
| O Contrário do Tempo | |||||
| Domador de Sonhos | |||||
|
|||||
|
Teoria A teoria das catástrofes (TC) nem sempre teve este nome, antes era falada mais correntemente como modelos matemáticos da morfogénese na designação preferencial que René Thom atribuiu [1], que buscara a expressão a partir dos trabalhos seminais de Alan Turing [2], arrumada no quadro da teoria matemática das singularidades de aplicações diferenciáveis num espaço euclideano, também entrosada na teoria das bifurcações. Trata-se de formas geométricas inseridas num quadro conceitual de sistemas dinâmicos: analisar fórmulas e as correspondentes geometrias de conjuntos singulares em espaços com vários parâmetros ou variáveis de controlo, e uma ou duas variáveis-resposta, associadas aos conceitos de função potencial e de dinâmica de gradiente num modelo físico: a bolinha desloca-se numa superfície lisa como descrita numa carta topográfica, com vales, encostas e cumes, e tende a buscar os sítios mais baixos, onde permanece, os equilíbrios estáveis; introduzindo perturbações, a bolinha pode deslocar-se de um vale para outro. As chamadas catástrofes elementares, ou conjuntos singulares de equilíbrios, no espaço-tempo euclideano com 4 parâmetros (4-D) são um total de 7 - já num espaço com 5 parâmetros passam a 11, e com 6 parâmetros tornam-se infinitas. De entre as 7 catástrofes elementares designam-se 4 com uma só variável-resposta, as cuspóides, e 3 com duas variáveis-resposta ou um vector bidimensional, as ombílicas [v. 3].
|
|||||
|
O ponto de partida da teoria, que é sobretudo física, é que a percepção está condicionada a formas estruturalmente estáveis, porque as outras dissipam-se antes de nos apercebermos sequer da sua existência, a que sucede a formulação de que um sistema físico observável então ocorre num ponto de equilíbrio de um campo potencial: o valor mínimo de uma função invisível que rege a sua dinâmica, o mais das vezes por derivação. Essa função potencial pode ser entendida como aquilo que Thom mais tarde vem a desenvolver no conceito de pregnância - os observáveis são saliências, formas salientes que emergem, que se ligam à pregnância como índices, indicam um invisível. A teoria das catástrofes tem assim um fundamento físico mais do que biológico, mas também tem relevância na biologia - foi aliás ao observar a transição de fase no zigoto de esfera para mórula e depois para gástrula, que Thom teve uma revelação: viu desdobrar-se a geometria de um dos modelos matemáticos da morfogénese. Rosa Branco coloca bem a análise quando afirma que a forma esquemática significa um modo de representar por meio de singularidades, reduzida a pontos de conteúdos condensados, potenciais [4], e que a TC procede sistematicamente à utilização das singularidades para explicar o salto brusco pelo qual uma forma emerge de um fundo contínuo. O termo ‘catástrofe’ foi vulgarizado pelo matemático britânico Christopher Zeeman, e outros, que sugeriram toda uma panóplia de descrições de observáveis, a tal ponto que fez moda fulgurante, a que se seguiu o desaire e a obliteração, porque afinal, como o próprio Thom recordava: uma teoria que explica tudo explica nada. A conotação negativa de catástrofe, que implica movimento de cima para baixo, de acordo com a interpretação mais corrente do radical grego katá, ocorre porque nos é mais fácil imaginar trajetos induzidos pela gravidade, comparados com aqueles que operam contra ela. Em fenómenos físicos de que os modelos da TC são descrições positivistas, seja as cáusticas formadas pela luz [v. 5] ou a marca de histerese nas curvas de absorção ou cedência de água do solo, não se vê a conotação negativa implicada, apenas a transição qualitativa de estados, também se poderia dizer emergência de novo e de sentido. À falta de melhor termo pode dizer-se que também existem catástrofes felizes: mais do que uma contradição está-se perante um oxímoro. Numa revisão recente do tema centrada nos efeitos de produção de sentido, afirma-se que a TC é o único modelo matemático que se provou adequado para as ciências naturais e para as ciências humanas ao mesmo tempo [6] - algo que nos remete para o assunto que Wilson definia como consiliência [7], a propósito da concordância de séries provindas de induções diferentes. No que sucede falo apenas de morfogénese, produção de formas, e também de semiogênese, produção de sentido, e os conjuntos característicos das cuspóides no espaço 4-D (dobra, cúspide, cauda de andorinha e borboleta) são designados conjuntos singulares [cf. 8]. O que se segue é um exercício de interpretação de elementos simbólicos, uma deriva onde os modelos morfogenéticos da cauda de andorinha e da borboleta ocupam lugar. O quadro mais geral desta pesquisa está balizado num enunciado metodológico [9]: a semiótica reconhece como sujeito verificável único do seu discurso a existência social do universo da significação, tal como é exibida pela verificabilidade física dos interpretantes, que são expressões materiais. Acresce que utilizo o conceito de hipótese como Peirce a formulou, visando a redução da multiplicidade, procurando inferir do resultado e do consequente o antecedente [10], e ainda que a hipótese não pode ser admitida sequer como hipótese a não ser que se suponha que dará conta dos factos ou pelo menos de alguns [11]. Como os objectos de pesquisa que se seguem são elementos ligados em semas arquitetônicos, vale ainda ressaltar que o objecto de arquitetura é realizado com materiais (sistema hilético) e funções técnico-físicas (sistema sintético) para um produto arquitetônico (sistema morfético) [12]. |
|||||
| Deriva | |||||
|
|||||
|
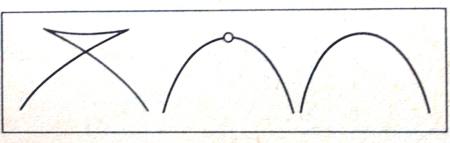
A passagem do arco de volta perfeita para ogival, uma metamorfose, poderá ser interpretada mediante algum modelo geométrico de inteligibilidade? A resposta é afirmativa, embora não se pretenda que seja única. O esquema seguinte (Fig. 2) apresenta cortes sequenciais do conjunto singular cauda de andorinha, que é uma superfície imersa no espaço tridimensional [v. 15]. No esboço apresentado quando se anda da direita para a esquerda transita-se pelo ponto cauda de andorinha no centro e alcança-se a secção que dá o nome à figura, onde a parte inferior, abaixo do ponto de cruzamento dos traços, tem forma ogival; a parte superior, em leque, é formada por duas cúspides ligadas. |
|||||
|
|
|||||
|
Fig. 2 – Esquema de cortes sucessivos no conjunto cauda de andorinha [16] |
|||||
|
|||||
| Esferas | |||||
|
|||||
|
O que parece típico no reinado de Manuel I não é apenas a presença da esfera armilar mas a sua replicação: esferas, duas em várias iluminuras de folhas de rosto de foral, seja o de Lisboa, reformado em 1500 [18] ou o de Bairro e Aguada. Também são duas as esferas armilares presentes na janela da sala do Capítulo do convento de Cristo e em portais de igrejas como no caso da Conceição Velha em Lisboa – esta é referida como exemplo numa das modalidades do veículo da arte renascentista: a ornamentação “ao romano” de edifícios que continuavam vinculados morfologicamente ao manuelino [19]. Podemos interrogar se neste estilo do período manuelino, variante do gótico flamejante, o arco ogival desapareceu de todo ou se está de alguma maneira remanescente. Aplicando o esquema da cauda de andorinha fixando as duas cúspides nas esferas armilares mostra-se que o arco ogival gótico poderá estar associado implicitamente à disposição dos elementos, à sintaxe da ornamentação do portal, envolvendo o tímpano que comporta o programa narrativo da Virgem da Misericórdia. |
|||||
 |
|||||
|
Fig. 5 – Diagrama da cauda de andorinha sobreposto no portal da igreja da Conceição Velha |
|||||
|
Essa replicação de esferas armilares pode suscitar várias hipóteses. Numa, a mais simples, já que D. Manuel fez da esfera o símbolo pessoal, a replicação é uma redundância, serve para enfatizar. Mas o paralelismo das esferas, também na janela do convento de Cristo, ou nos Jerónimos ladeando o escudo de armas, ou outros, ainda se pode interpretar como uma menção a mundos paralelos. No caso, é provável que subsuma a declaração de existência do Novo Mundo para Ocidente do meridiano de Tordesilhas, correspondente ao tratado assinado e ratificado em 1494, e aprovado pelo papa Julio II em 1506, de par com o velho mundo que seguia para Oriente e que era declarado conhecido [v. 20] Em 1537 Pedro Nunes publicava o Tratado da Sphera, a tradução cuidada da obra de Sacrobosco e a versão do Livro I da Geografia de Ptolomeu, e da Teórica do Sol e da Lua de Purbáquio, a que acrescem dois textos originais: o Tratado de Certas Dúvidas de Navegação e o Tratado em Defensão da Carta de Marear [21]. Pedro Nunes foi um matemático notável, já depois de jubilado da Universidade de Coimbra foi convidado pelo papa Gregório XIII para se pronunciar sobre a reforma do calendário juliano, em 1577, e, antes, em 1575 presidira à reforma do sistema de pesos e medidas de D. Sebastião. Nesse esboço que consta na sua obra (fig. 6) distingue-se o mundo oriental que se esfuma nas ilhas, enquanto o Brasil espreita a Ocidente e os paralelos numerados eram designados de climas. |
|||||
|
|
|||||
|
Fig. 6 - Tratado da Sphera de Pedro Nunes, 1537 |
|||||
|
|||||
|
Na hipótese de a borboleta ser pertinente na leitura daquele portal que podemos indagar? De uma esfera nascem duas ou coexistem as três em simultâneo? Coexistem no portal, é um facto, mas a leitura principal é vectorial, a ascenção vertical, e daí poder-se inferir que é como se de um mundo emergissem dois em paralelo - como se fora uma mitose celular? A aposição do esquema da borboleta sobre o portal é abdutiva, outros considerarão arbitrária, mas abdução é o procedimento que se exemplifica extremadamente com o caso da descoberta por Cardano (c. 1545) dos números imaginários, que, à falta de comensurabilidade com os restantes, considerou estarem numa superfície ausente. |
|||||
| Coda | |||||
|
Pensar é espacializar, espacializar é classificar e a panorâmica do ver é categorial [ v. 25], eis um mote que está conforme a esta digressão, e estesia quer dizer percepção – o espaço onde o corpo é de certo modo perceptivamente empenhado com o mundo e o habitat [26]. Se os modelos da cauda de andorinha e da borboleta são pertinentes na leitura dos portais, fica levantada uma questão: os esquemas foram utilizados numa aplicação sintáctica, na ligação e disposição de elementos arquitetônicos - qual será a semântica que lhe estará associada? Petitot refere que a sintaxe dos juízos tem a ver com os tipos, e a semântica com a localização, no sentido de reportar-se às condições de verdade associadas aos fenómenos de cobertura de domínios espaciais por qualidades [27]. Um tipo é formado por caracteres (tupos) e traduz-se numa classe de signos que informam um código, declarativo ou votivo, um sistema de modelização do mundo [v. 28]. Enquanto conjuntos singulares na teoria dos sistemas dinâmicos a cauda de andorinha remete para uma função potencial com dois equilíbrios estáveis, um instável, e um abismo, enquanto que a borboleta indexa três equilíbrios estáveis, separados por dois instáveis. Petitot descreve a cauda de andorinha como um sistema de indicadores – um modelo de deixis -, e a borboleta é referida na linguística como permitindo modelizar o verbo dar [29]. São múltiplos os nomes da figura feminina coroada que centraliza os portais: Virgem com o Menino, Nossa Senhora do Bom Sucesso, Salvé Rainha, outros, e parece remeterem em qualquer caso para a sacralização da Vida dentro de programas iconográficos cristãos, mas a que se pode associar uma raíz pagã. A mulher coroada num capitel da entrada principal da Sé pode representar Cibele, a Grande Mãe, por entre folhagem, ostentando coroa em forma de torre aberta [30], de que há testemunho do culto na forma de dois monumentos epigráficos encontrados perto – a deusa era representada por uma pedra negra no seu local de origem, Pessinonte, a norte de Éfeso, na Ásia Menor e foi assimilada a Artemisa-Diana, irmã de Apolo, também este referido como provável objecto de culto na vizinhança do sítio da Sé de Lisboa. |
|||||
|
|||||
| Referências | |||||
|
[*] Umberto Eco, A Estrutura Ausente (7ª ed.), Perspectiva Editora SA, São Paulo, 2007, p:353. [&] Jean Petitot, Le hiatus entre la logique et le morphologique. Prédication et perception. In Semiosis and Catastrophes – René Thom’s Semiotic Heritage, (W. Widen & Per Aage Brandt, eds.), Peter Lang, Bern, 2010, v. 10: 141-166. [§]Rosa Alice Branco, A conceptualização da forma na teoria das catástrofes, Revista da Faculdade de Letras da Universidade do Porto, série Filosofia, vol 5-6, segunda série, 1988-89, p: 481-500. http://ler.letras.up.pt/uploads/ficheiros/1705.pdf [1] René Thom, Modèles Mathématiques de la Morphogénèse (2 éd.), Christian Bourgois Editeur, Paris, 1980, 315 p. [2] Alan Turing, The chemical basis of morphogenesis, Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, Vol. 237, No. 641. (Aug. 14, 1952), pp. 37-72. http://www.dna.caltech.edu/courses/cs191/paperscs191/turing.pdf [3] http://mathworld.wolfram.com/Catastrophe.html [4] Rosa Alice Branco, idem. [5] http://www.triplov.com/casquilho/2008/Causticas-de-luz/index.html [6] Ángel López-García, Catastrophes: what are we talking about? In Wolfgang Wilden & Per Aage Brandt (eds.), Semiosis and catastrophes - René Thom’s semiotic heritage, Peter Lang, Bern, vol. 10, 2010, p: 127-138. [7] Edward O. Wilson, Consilience - La Unidad del Conocimiento. Galaxia Gutenberg, Barcelona, 1999, 485 p. [8] Peter T. Saunders, Catastrophe Theory, Cambridge University Press, Cambridge, 1980, 144 p. [9] Umberto Eco, Tratado Geral de Semiótica (4ª ed.), Perspectiva Editora SA, São Paulo, 2007, p: 258. [10] Ana Paula Silva, Metamorfoses do conceito de abdução em Peirce – o exemplo de Kepler, Centro de Filosofia das Ciências da Universidade de Lisboa, Lisboa, 2009, 269 p. [11] Albrecht Heeffer, Abduction as a strategy for concept formation in mathematics, in Abduction and the Process of Scientific Discovery (ed. Olga Pombo & Alexander Gerner) Centro de Filosofia das Ciências da Universidade de Lisboa, Lisboa, 2007, p: 179-194. [12] Elisabeth Walther-Bense, A Teoria Geral dos Signos – introdução aos fundamentos da semiótica, Editora Perspectiva SA, São Paulo, 2000, 128 p. [13] http://novaserie.revista.triplov.com/ana_luisa_janeira/jose_casquilho/index.html [14] Eduardo Sucena, A Sé Patriarcal de Lisboa – História e Património, Sete Caminhos Produções Editoriais Lda, Lisboa, 2004, p:25 [15] http://www.triplov.com/casquilho/2009/Morfogenese/index.html [16] Arnold, V. I., Catastrophe Theory (2nd ed.), Springer-Verlag, Berlin, 1986, p:30. [17] Eduardo Sucena, idem, p: 27 [18] Lisboa Quinhentista – a imagem e a vida da cidade (catálogo de exposição, coord: Irisalva Moita), Museu da Cidade, ed. CML, 1983, p: 132 [19] Joaquim Veríssimo Serrão, História de Portugal, vol. III: o século de ouro [1495-1580] (2ª ed.), Editorial Verbo, Lisboa, 1988, p: 398 [20] http://pt.wikipedia.org/wiki/Tratado_de_Tordesilhas [21] A. A. Marques de Almeida, Catálogo: O Mundo de Pedro Nunes e de Damião de Góis – a diferença dos olhares entre o inovar e o resistir, 1502-1578. Comissão Nacional para as Comemorações dos Descobrimentos Portugueses, Lisboa, 2002, p: 68 [22] José Casquilho, Figuras do tempo in Leituras do Tempo (coord: Almerindo Lessa), Universidade Internacional, Lisboa, 1990, p: 30-40. [24] Luís Maria Pedrosa dos Santos Graça, Convento de Cristo, ELO – Publicidade, Artes Gráficas Lda, 1994, p: 48. [25] http://triplov.org/novaserie.revista/ana_luisa_janeira/ana_luisa_janeira/ultima-aula.html [26]José Augusto Mourão, A estética na fronteira da experiência de Deus. Encontros do Lumiar 2010-2011, p:3. [27] Jean Petitot, idem.
[28]http://www.arte-coa.pt/index.php?Language=pt&Page=Saberes&SubPage=ComunicacaoELinguagem [29] Ángel López-García, idem. [30]Eduardo Sucena, idem, p: 46 |
|||||
|
|
|||||
|
José Pinto Casquilho (Portugal) |
|||||
|
|
|||||
|
© Maria Estela Guedes |
|||||